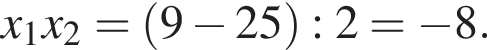Среди значений переменной х, равных 10; 20; 50; 105; 100, укажите то, при котором значение функции  больше 10.
больше 10.
РЕШУ ЦТ — математика ЦЭ
Вариант № 150
1.
i
1) 10
2) 20
3) 50
4) 105
5) 100
2.
i
На рисунке изображена правильная четырехугольная пирамида. Среди отрезков SB, MQ, SM, SO, MN укажите отрезок, который является апофемой правильной четырехугольной пирамиды.
1) SB
2) MQ
3) SM
4) SO
5) MТ
3.
i
Если 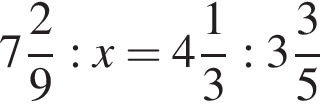 — верная пропорция, то число x равно:
— верная пропорция, то число x равно:
1) 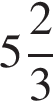
2) 
3) 
4) 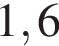
5) 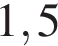
4.
i
Найдите градусную меру угла, смежного с углом, радианная мера которого равна ![]()
1) 46°
2) 42°
3) 50°
4) 45°
5) 48°
5.
i
Укажите номер выражения, являющегося одночленом восьмой степени:
а) 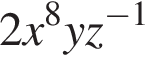 | б) 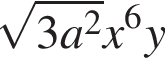 | в) | г) 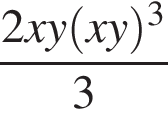 | д) |
1) а
2) 6
3) в
4) г
5) д
6.
i
Окружность задана уравнением 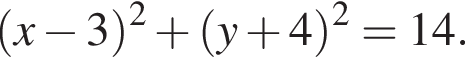 Укажите номер верного утверждения.
Укажите номер верного утверждения.
1) Точка A(-4; 3) лежит на окружности;
2) Центром окружности является точка О(-3; 4);
3) Диаметр окружности равен 14;
4) Прямая 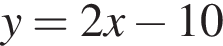 проходит через центр окружности;
проходит через центр окружности;
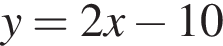 проходит через центр окружности;
проходит через центр окружности;5) Радиус окружности равен 7.
7.
i
Найдите площадь фигуры, изображенной на рисунке.
1) 35,5 см2
2) 28 см2
3) 36 см2
4) 49 см2
5) 35 см2
8.
i
Результат упрощения выражения 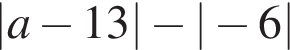 при
при  имеет вид:
имеет вид:
1) 
2) 
3) 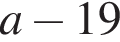
4) 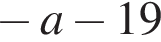
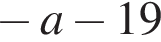
5) 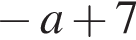
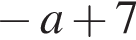
9.
i
Значение выражения 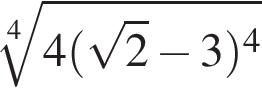 равно:
равно:
1) 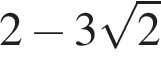
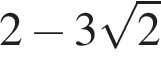
2) 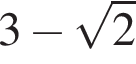
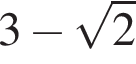
3) 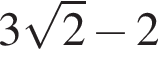
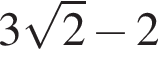
4) 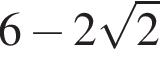
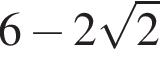
5) 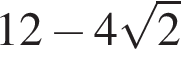
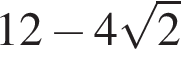
10.
i
Пусть x1 и x2 — корни уравнения 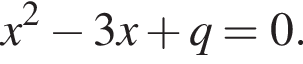 Найдите число q, при котором выполняется равенство
Найдите число q, при котором выполняется равенство 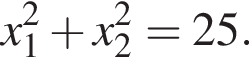
1) -8
2) -3
3) 8
4) 4
5) -5

 — неверно;
— неверно; — неверно;
— неверно; — неверно;
— неверно; — верно;
— верно; — неверно.
— неверно.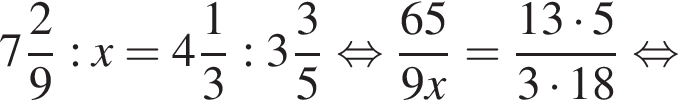
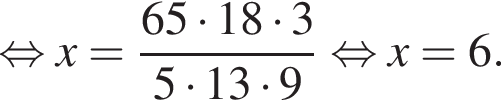
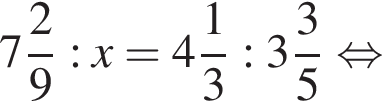
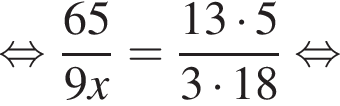
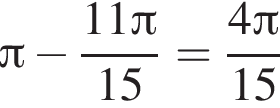 или 48°.
или 48°.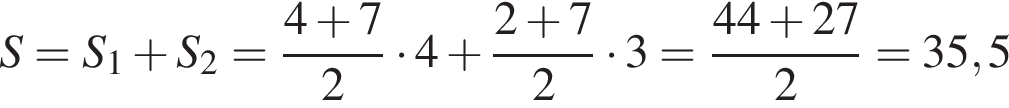
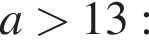
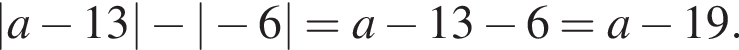
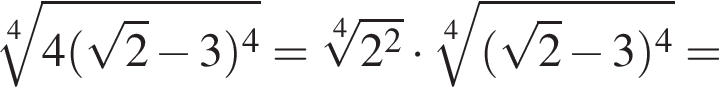
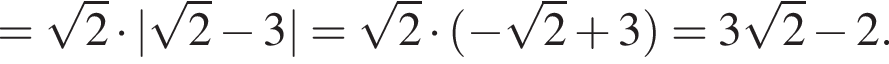

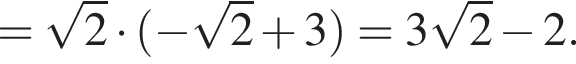
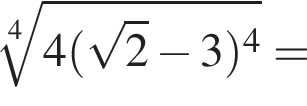
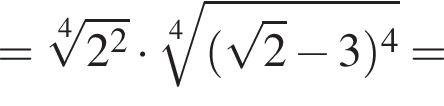
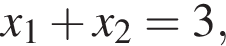 а
а 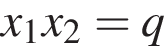
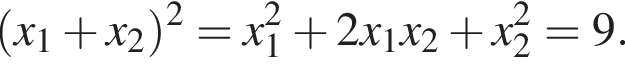 Зная то, что
Зная то, что